TEMA 8

OPERACIONES CON FRACCIONES

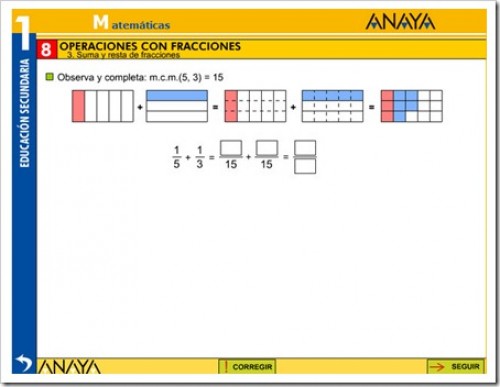
1. SUMA Y RESTA DE UNIDADES ENTERAS Y FRACCIONES.

2. SUMA Y RESTA DE FRACCIONES.

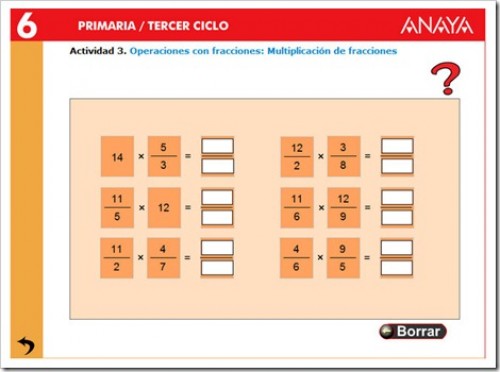
3. PRODUCTO DE FRACCIONES.

4. COCIENTE DE FRACCIONES.

5. REPASO LA UNIDAD.

1. SUMA Y RESTA DE UNIDADES ENTERAS Y FRACCIONES.

Pincha en el enlace y observa qué otras situaciones, en las que debes emplear las fracciones, existen en la vida real.

$fracciones.operaciones$

Recuerda cómo puedes reducir o simplificar una fracción.

$fracciones irreducibles$

SUMA DE FRACCIONES

$suma de fracciones$

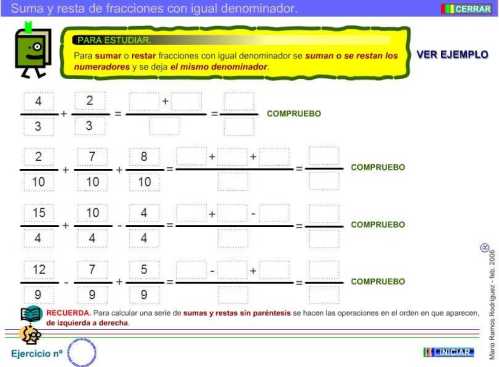
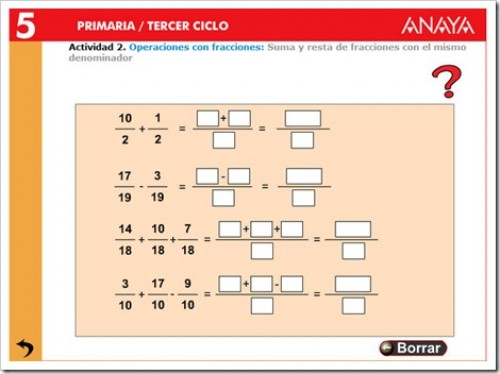
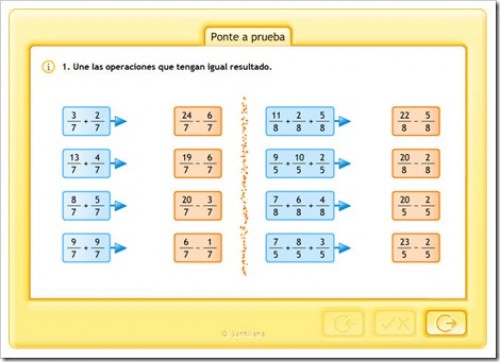
SUMAS Y RESTAS CON EL MISMO DENOMINADOR

$sumafracciones$

SUMA DE FRACCIONES CON DISTINTO DENOMINADOR

MÉTODO DE LOS PRODUCTOS CRUZADOS

MÉTODO DEL MÍNIMO COMÚN MÚLTIPLO

$Suma de fracciones con distinto denominador$

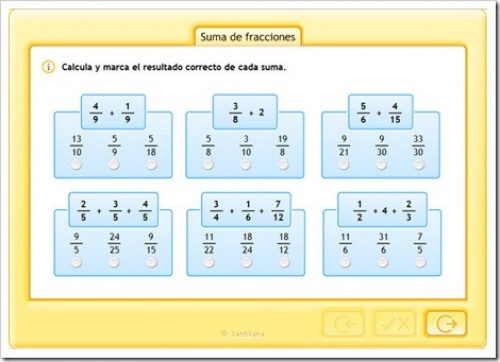
RESTAS CON DISTINTO DENOMINADOR (PRODUCTOS CRUZADOS)

$Resta de fracciones con distinto denominador$

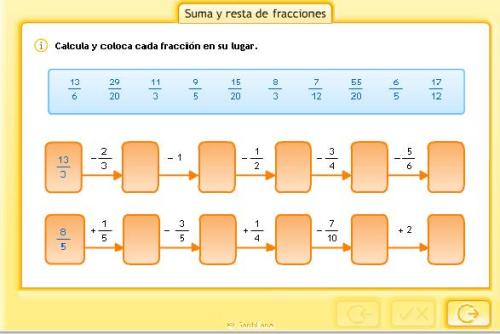
$Suma y resta de fracciones$

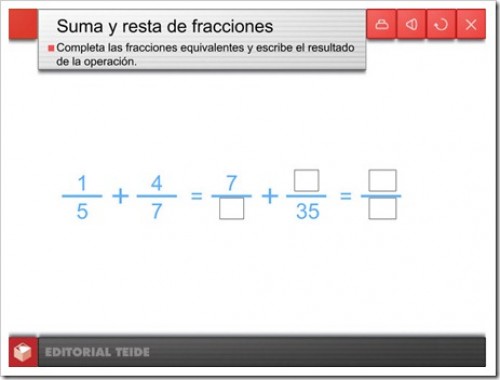
SUMA Y RESTA DE FRACCIONES CON DISTINTO DENOMINADOR

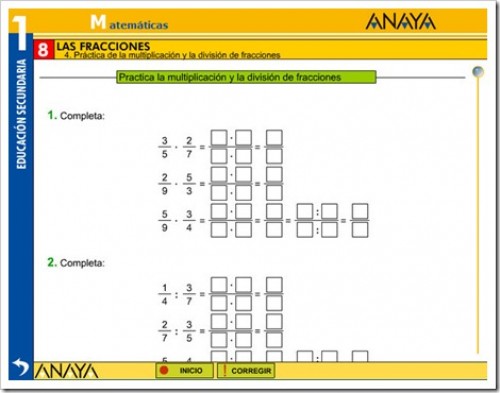
MULTIPLICACIÓN DE FRACCIONES

$Multiplicación de fracciones$

$multiplicar-un-nmero-por-una-fraccin$

$multiplicación de fracciones$

DIVISIÓN DE FRACCIONES

$división de fracciones$
$división de fracciones$

$problemas con fracciones$

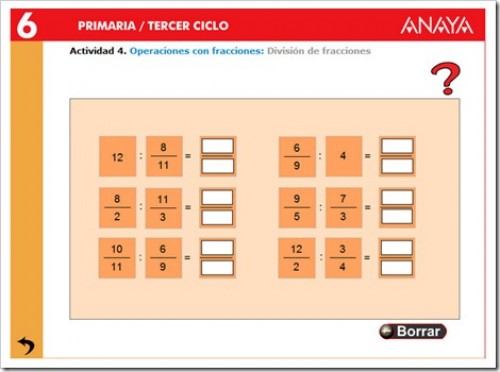
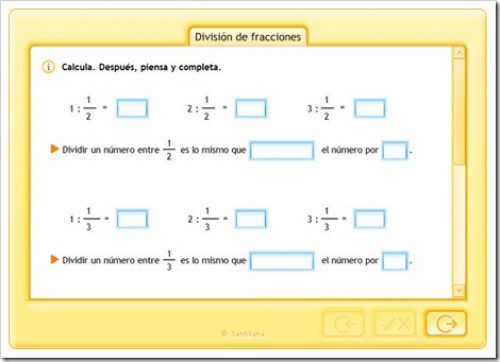
$divisin-fracciones1$
$multiplicacin-y-divisin-de-fracciones$

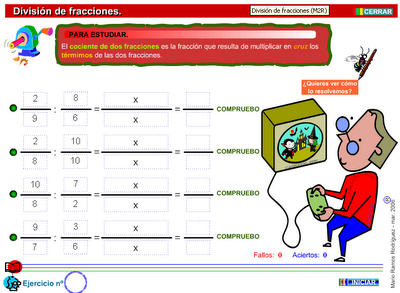
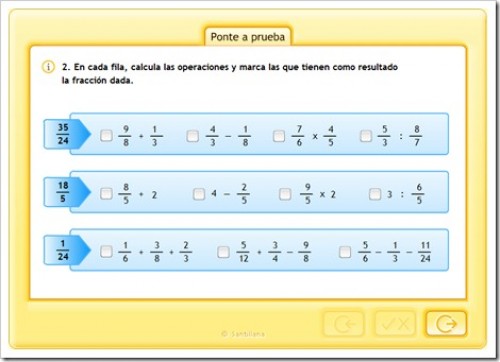
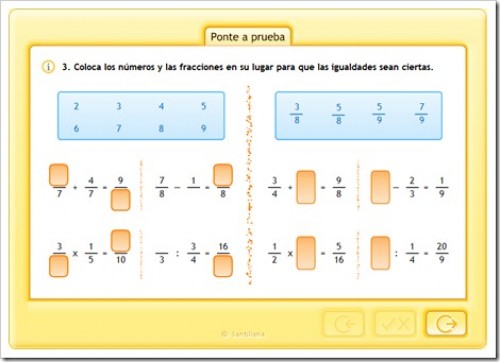
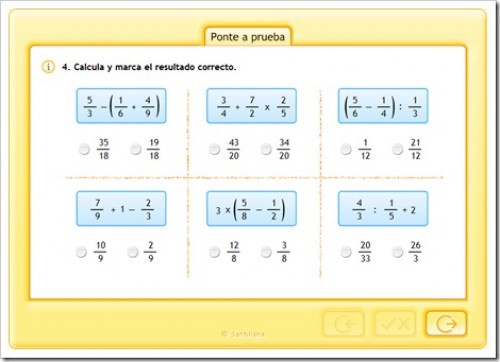
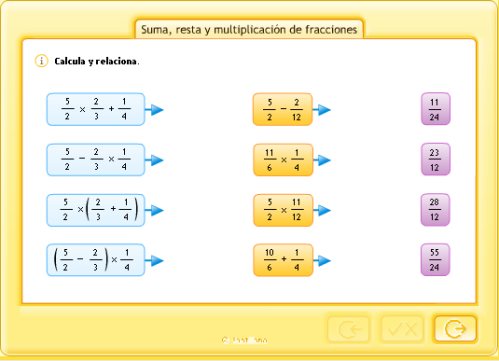
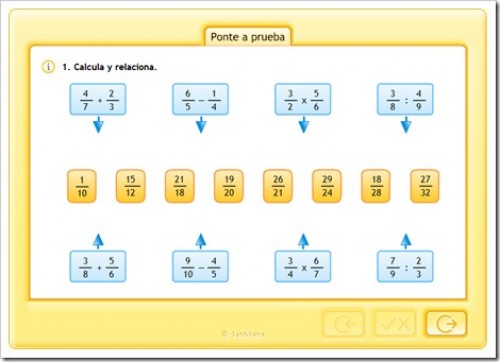
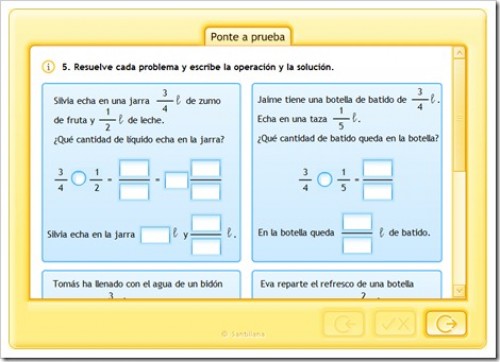
PONTE A PRUEBA

ERES CAPAZ DE…

REPRESENTAR LA SITUACIÓN

$problemas_con_fracciones8$

PROBLEMAS CON FRACCIONES

RESUELVE EL SIGUIENTE PROBLEMA

$fracciones$

$problemas con fracciones1$ $problemas con fracciones2$ $problemas con fracciones3$ $problemas con fracciones4$ $problemas con fracciones5$ $problemas con fracciones6$ $problemas con fracciones7$

OPERACIONES CON FRACCIONES
.

1.- Fracciones de una cantidad

Para calcular la fracción de una cantidad se multiplica la cantidad por el numerador y se divide por el denominador.
Veamos un ejemplo:

Multiplicamos 20 por el numerador: 20 x 5 = 100
El resultado lo dividimos por el denominador: 100 : 6 = 16,66

Luego:

2.- Suma y resta de fracciones

Para sumar y restar fracciones hay que distinguir entre:

Fracciones con igual denominador
Fracciones con distinto denominador

a) Fracciones con igual denominador

En este caso para sumar o restar fracciones se mantiene constante el denominador y se suman o restan sus numeradores.
Veamos un ejemplo:

Sumamos sus numeradores y mantenemos el denominador:

Veamos otro ejemplo:

Restamos sus numeradores y mantenemos el denominador:

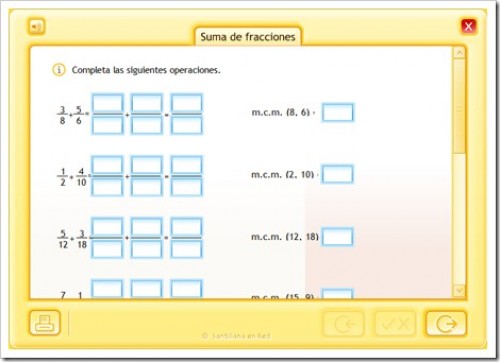
b) Fracciones con distinto denominador

En este caso para sumar o restar fracciones:

Lo primero que hay que hacer es buscar un denominador común a todas ellas.
Luego sustituir las fracciones originales por fracciones equivalentes con este denominador común.

Y ¿cómo se calcula este denominador común? utilizaremos el método del mínimo común múltiplo (MCM).
Una vez obtenido el denominador común hay que calcular las fracciones equivalentes. Para cada fracción haremos lo siguiente.

Sustituimos su denominador por el denominador común.
Calculamos su numerador de la siguiente manera: dividimos el denominador común por el denominador original de cada fracción. El resultado obtenido lo multiplicamos por el numerador original, obteniendo el numerador de la fracción equivalente.

Es más fácil ver todo esto con un ejemplo:

Vamos a calcular las fracciones equivalentes:

Primero calculamos el denominador común: si calculamos los múltiplos de 4, de 3 y de 5 vemos que el MCM es 60.

Ahora vamos a calcular el numerador equivalente de cada fracción:
Primera fracción:

Dividimos el denominador común entre su denominador: 60 : 4 =15
Multiplicamos este resultado por su numerador: 15 x 2 = 30
Segunda fracción:

Dividimos el denominador común entre su denominador: 60 : 3 = 20
Multiplicamos este resultado por su numerador: 20 x 6 = 120
Terecra fracción:

Dividimos el denominador común entre su denominador: 60 : 5 =12
Multiplicamos este resultado por su numerador: 12 x 3 = 36

Ya podemos sustituir las fracciones originales por sus fracciones equivalentes:

Y procedemos a la suma:

Ejercicios

(En los ejercicios para ver la solución hacer click en recuadro; doble click vuelve a la posición original)

1.- Resuelve la siguientes operaciones:

2.- Resuelve la siguientes operaciones:

OPERACIONES CON FRACCIONES (cont.)

1.- Multiplicación de fracciones
.
Para multiplicar fracciones:

Se multiplican sus numeradores y sus denominadores:

Vamos a ver otros ejemplos:

2.- División de fracciones
.
Cuando se dividen 2 fracciones:

La fracción resultante tendrá:

Como numerador: el resultado de multiplicar el númerador de la primera por el denominador de la segunda.
Como denominador: el resultado de multiplicar el denominador de la primera por el numerador de la segunda.